Powers of a permutation matrix - Part 3

Published on 22 Nov 2023, under:  | mathematics |  linearalgebra |  permutations |   

In Part 2, we saw how permutations consisting of simple cycles always return to their original configurations. Now let’s consider a permutation p, consisting of m number of cycles, with sizes k₁, k₂, … k_m, such that

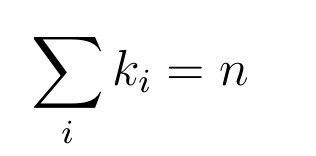
and no two cycles are of the same length. For such a permutation we have

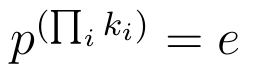
since any cycle will return to it’s original position at the q times kth application of p (where k is the length of the cycle), which means that all cycles in the permutation will return to their original positions when the permutation is applied

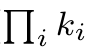
times.

But what if the cycles are not all of the cycles are of different lengths? In that case we only need to consider the unique lengths among the various cycle lengths. That is, if the permutation consists of one 2-cycle, three 5-cycles, two 3-cycles, and two 7-cycles, then the permutation will return to it’s initial configuration at the 2 x 5 x 7 x 3 = 210th application of the permutation. This is easy to see becuase if there are l cycles of length k, all of them will return to their starting configuration at every kth application of the permutation. Once again I’m ignoring situations where one cycle is a of a length that is a multiple of another cycles length, since the other cycle will in any case return to it’s original position when the larger cycle returns to it’s original position. The thing it would impact is the smallest number N such that p^N = e. I’m not sure how to go about tackling that.

One question remains - Can all permutations be represented as collections of cycles. To see why the answer is yes, consider that any permutation has at least one cycle. Let’s assume that a permutationhas m cycles, with fixed points being cycles of length 1. Now imagine that there are some elements in the set being permuted that do not belong to either of the m cycles. If we now apply the permutation to just these points, then either they retain their positions, making them fixed points which is a contradiction, or they do move to different positions, implying that there is a cycle of size at least two, which is also a contradiction. This means that every permutation has to be composed of cycles.

One last note - I posted about powers of permutations on reddit, and a user asked if anything can be said about p^n! where n is the number of elements being permuted. Since the lengths of the cycles that make up any permutation will always be lesser than or equal to the number of elements in the set, n! will include all the cycle lengths in the product. So p^n! will also be the identity. So there was a much simpler way to show that such a number exists. But it is not necessarily the smallest number such that p^N is the identity. I am fairly confident that the smallest number N with this property is the least common multiple of (n, n-1, n-2, …, 1) but I don’t know how to prove it.