Order of the Power Set
Published on 10 Oct 2023, under:Here are two ways to determine the number of elements in the Power set of a finite set of objects. The set of all subsets of a set is called a power set, and the number of all the elements in a given set is called its order. Consider the following set S = {a, b, c}. The order of this set is 3, and its power set is P(S) = {O, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, S}. Notice that the power set contains all subsets of S, including S, and the empty set O. We can see that P(S) has 8 elements, so its order is 8. If you carried out a similar exercize for a set S’ = {a, b, c, d}, we will find that its order is 16. It looks like the order of a the power set of a set with n elements is 2n.
We can show that this is actually true. Let’s prove it in two ways. First let’s use mathematical induction, which is intuitive and clean, but a little dry IMO. Next, let’s show that it is true by just counting the elements (kind of). This is a lot more fun, and it’s nice to see how a couple of things come together to solve the problem.
But first let’s do induction. Notice that if a set S is empty, it has n = 0 elements. The power set, P(S), then only has one element - the empty set (which is also the entire set S). So the order of the power set is 1, and 20 = 1, so the base case is true. Now let’s assume that it is true for the power set of a set with n elements. So the power set of a set with n elements would have order 2n. Let’s denote the elements of the power sets as S1, S2, …, Sm, where m = 2n. Now consider adding one more element to S, bringing the number of elements contained by it to n+1. Adding this additional element to S creates a whole bunch of new subsets, and we have to determine how many new subsets are created and add it to 2n, to find the order of the new power set of S. Notice that all the new subsets of S can be created by adding the new element to each of the subsets of S with n elements.
For example, if S = {a, b}, then P(S) = {O, {a}, {b}, S}. If we add a third element, c, to this set, then we get the new subsets -
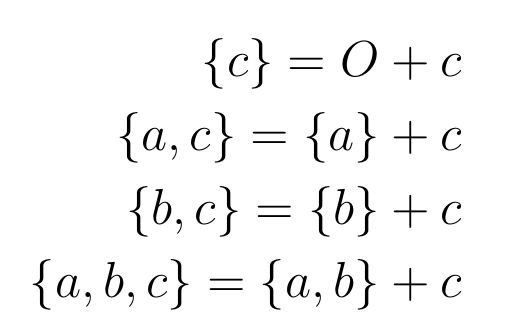
Essentially, by adding an additional element to S, we are adding one additional subset to every subset in power set of the original set. So we have two times as many elements in the power set of a set with n+1 elements, as in the power set of one with n elements. That is, the order of the power set of a set with n+1 elements is 2 x 2n = 2n+1, and we are done.
Now let’s do it the fun way. Notice that we can determine the number of subsets of a set with n elements by counting the number of subsets with 0 elements (the empty set), the number of subsets with 1 element (these are called singletons, there are n of them), with 2 elements and so on, up to the number of subsets with n elements (there’s one such subset - the entire set), and then adding them all up. To do this, let’s find the number of subsets with k elements. This is equivalent to the number of ways of choosing k objects from a collection of n objects. We know that this is
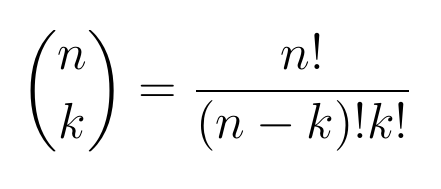
Now we have to sum the number of subsets with k elements from k = 0 to k = n. That is, the order of the power set is
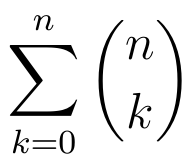
All that is left to do is to evaluate this sum. It looks a little intimidating, and trying to evaluate it by expanding the sum and adding all the terms will turn out to be quite an effort. So maybe there’s another way. Notice that the sum looks remarkably similar to the sum in the binomial theorem:
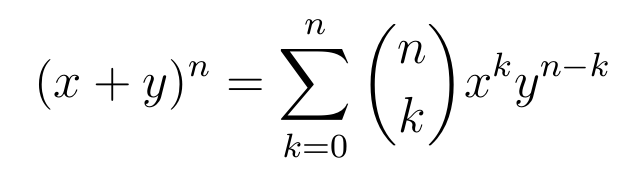
In fact if we set x = y = 1 in the binomial theorem, the sum will be the same as the sum in our expression for the order of the power set,
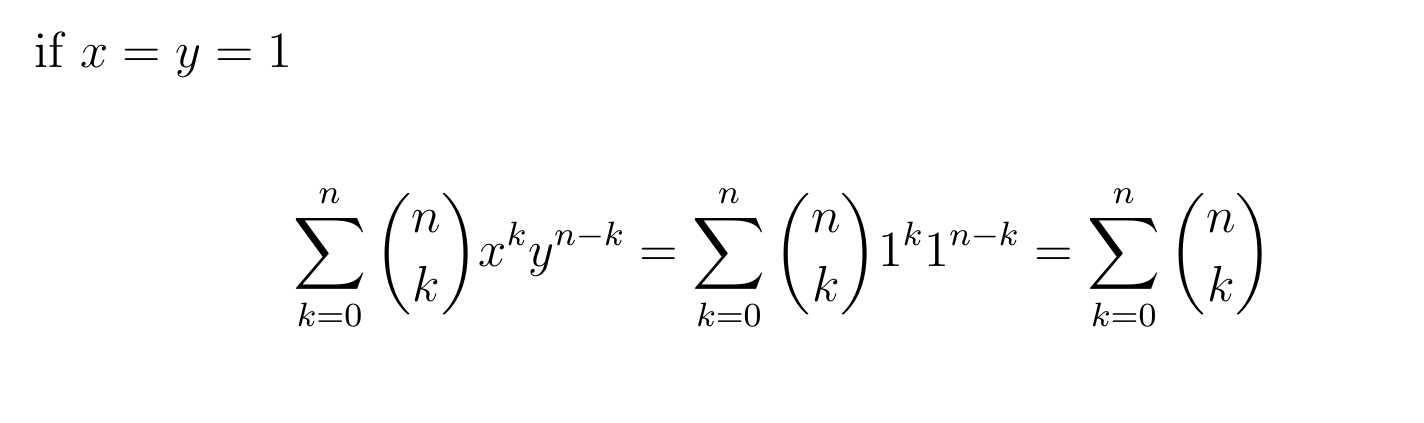
and
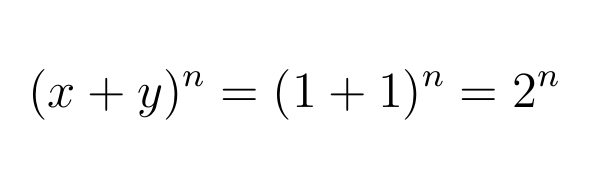
which means
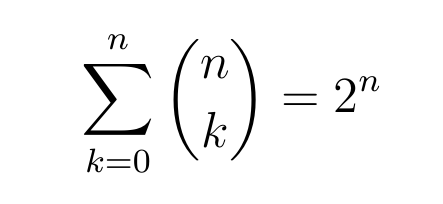
and we’re done!