An interesting infinite series

An area of mathematics with which I had a lot of trouble was infinite sequences and series. To address this I have been practicing by solving a bunch of problems on this topic. Here’s an interesting, if somewhat simple, problem I came across -

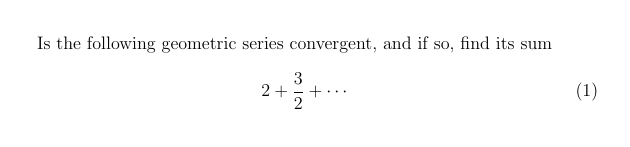
To recap, a geometric series is an infinite series of the form

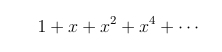
and if |x| < 1, the series converges, and the sum of the series is 1 / (1 - x). To get a better idea of (1), let us write out a few more terms of the series. As we are told that it is a geometric series, it seems reasonable to assume that the series looks like this

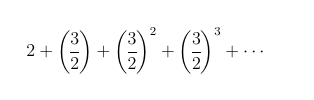
At first glance, series (1) does not really look a geometric series, as the first term is not 1. However, we could rewrite the series in the following fashion

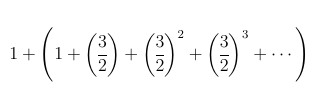
This way, the series inside the parentheses is geometric, with x = 3/2. Since 3/2 > 1, we can conclude that this series does not converge, and hence the original series does not converge either. So that’s that. But what if we played around with the constraints a little bit? What if the series was not geometric? In that case, the first thing we have to do is figure out the structure of the new series. Since all every term of an infinite series has to be is a definite number, x_n, for every positive number n, we have a lot of freedom in choosing how to build this series.^[1] For example,

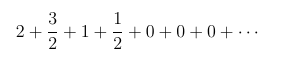
would be an infinite series that isn’t geometric. This is not very interesting however, since it is immediately clear that the series converges with a sum of 5. To make the job of constructing the series a little easier, let us insist that the nth term of the series, x_n be expressable as some (hopefully simple) formula. So the following series

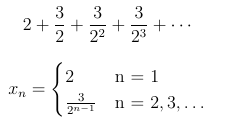
satisfies the requirement, but it’s not all that interesting (it’s almost geometric). The series converges with the sum coincidently also equal to 5.

How about this one -

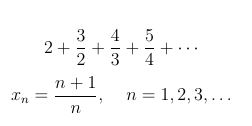
I like this one. The nth term is expressable as a simple formula, and it does not have any special cases, unlike the previous example. This series however does not converge. It gets an A-.

Let’s try one last series that could fit the first two terms of the series from the problem -

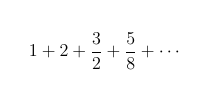
This series doesn’t look a lot like the one with which we started off. For one thing, the series progresses by increasing from one to two, and then decreases to 3/2 and decreases again to 5/8. Given that that last three terms are decreasing, we can get away with assuming that the rest of the terms in the series decrease too. In fact, if we re-arrange the series like this -

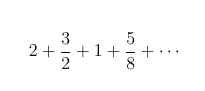
we can see that the give terms do all decrease. Now, by observing that we can write 1 as 4/4, 4 as 2², and that 8 as 2³, the series becomes

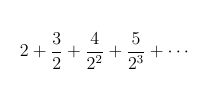
Now it is clear that

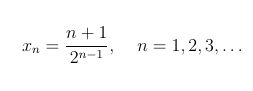
Here too, we have a nice simple formula without any special cases. As an added bonus, this series also converges (to see why, observe that the series of partial sums increases, the nth partial sum is bounded above by 2(n+1), and an increasing series that is bounded always converges). To find the sum to which the series converges, we will let S represent the sum. Since x_n = (n + 1) / 2^n-1 = (n / 2^n-1) + (1 / 2^n-1), we have

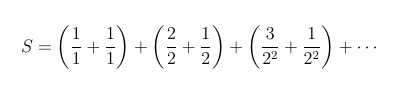
which we can be rearranged like so -

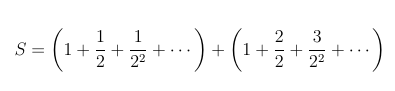
We are more or less done now, since the series in the first parentheses on the right hand side of the equation is the geometric series with sum 1 / (1 - 0.5) = 2, and as for the series on the second pair of parentheses, note that

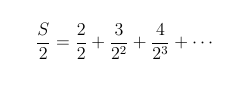
So we have S = 2 + (1 + S / 2) and solving for S gives us

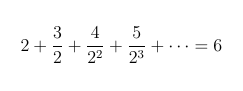
^[1] Calculus with Analytic Geometry, Simmons, George F., Chapter 13, pp 432, 439

Problem solving and mindfulness

I wanted to write a little something about a change I noticed in the way I usually respond when I find myself unable to find a solution to a problem. A few weeks ago I was trying to solve this problem

After working on it off and on for a few days, I hit upon the key idea that solved it just as I was falling asleep.

I don’t think it’s a very tough problem, however I had quite some trouble cracking it. Luckily there was a hint, and I was able to make some progress, but I got stuck soon after. I started to feel a familiar sense of frustration and a strong desire to give up and look the solution up. In the not so very distant past, I would have succumbed and looked the solution up, and then immediately felt insecure about it.

This time, I told myself that I should put it away for the day and give it another shot later. I started working on it again the next day, when a different approach suggested itself and I was able to go a little further. This surprised me because my usual practice is to try the same thing over and over again and then get frustrated when it doesn’t work. Eventually, when the intrusive thoughts, “It’s hopeless”, “I told you, you’re horrible at math”, “stop fooling yourself”, inevitably won, I would give up and be depressed for a while.

Recently however, I am noticing that I have been able to avoid this mental road block. It’s not that the thoughts aren’t there, they are ever present, but I’ve been getting better at keeping at it even with the circling negativity. I have observed that if I acknowledge the negative thought (or just ignore it) and try again, more often than not, I find the solution to the problem, or I think of a different approach to finding it. It almost feels like the I had the answer all along, but I couldn’t find it because of all the cacophony in my head. But if I take a moment to relax, maybe do the 4x4 breaths technique, I find the way forward.

Another factor is the complete lack of time pressure. I have no assignment deadlines, or timed exams where I have to solve problems in a finite amount of time. I’m doing this as a hobby, and I can take all the time I need. Without all the anxiety to finish in time, it’s a lot easier to think of alternative approaches to problem solving. Sure, sometimes I feel insecure about spending whole days to solve a relatively simple problem, but hey, instead of giving up and feeling sad about it, I’m finding answers and feeling a sense of joy and accomplishment.

Powers of a permutation matrix - Part 3

In Part 2, we saw how permutations consisting of simple cycles always return to their original configurations. Now let’s consider a permutation p, consisting of m number of cycles, with sizes k₁, k₂, … k_m, such that

and no two cycles are of the same length. For such a permutation we have

since any cycle will return to it’s original position at the q times kth application of p (where k is the length of the cycle), which means that all cycles in the permutation will return to their original positions when the permutation is applied

times.

But what if the cycles are not all of the cycles are of different lengths? In that case we only need to consider the unique lengths among the various cycle lengths. That is, if the permutation consists of one 2-cycle, three 5-cycles, two 3-cycles, and two 7-cycles, then the permutation will return to it’s initial configuration at the 2 x 5 x 7 x 3 = 210th application of the permutation. This is easy to see becuase if there are l cycles of length k, all of them will return to their starting configuration at every kth application of the permutation. Once again I’m ignoring situations where one cycle is a of a length that is a multiple of another cycles length, since the other cycle will in any case return to it’s original position when the larger cycle returns to it’s original position. The thing it would impact is the smallest number N such that p^N = e. I’m not sure how to go about tackling that.

One question remains - Can all permutations be represented as collections of cycles. To see why the answer is yes, consider that any permutation has at least one cycle. Let’s assume that a permutationhas m cycles, with fixed points being cycles of length 1. Now imagine that there are some elements in the set being permuted that do not belong to either of the m cycles. If we now apply the permutation to just these points, then either they retain their positions, making them fixed points which is a contradiction, or they do move to different positions, implying that there is a cycle of size at least two, which is also a contradiction. This means that every permutation has to be composed of cycles.

One last note - I posted about powers of permutations on reddit, and a user asked if anything can be said about p^n! where n is the number of elements being permuted. Since the lengths of the cycles that make up any permutation will always be lesser than or equal to the number of elements in the set, n! will include all the cycle lengths in the product. So p^n! will also be the identity. So there was a much simpler way to show that such a number exists. But it is not necessarily the smallest number such that p^N is the identity. I am fairly confident that the smallest number N with this property is the least common multiple of (n, n-1, n-2, …, 1) but I don’t know how to prove it.